Hanojské věže
Hanojské věže jsou logická úloha s jednoduchým zadáním, ale širokými možnostmi využití. Používá se v kognitivní vědě při zkoumání způsobů, jak lidé řeší problémy, a v informatice při výuce principu rekurze. Obtížnost úlohy lze plynule přizpůsobovat podle počtu disků a zvolené varianty. Úlohu je navíc možné snadno ztvárnit naživo a využít ji jako týmový úkol.
Základní úloha
Legenda
Kdesi v horách nedaleko města Hanoj stojí chrám, ve kterém je velká místnost a v ní 64 zlatých disků různých velikostí. V místnosti jsou umístěny tři kolíky, mezi kterými mniši zlaté disky přesouvají. Až se mnichům podaří v souladu s pravidly přemístit všechny disky z prvního kolíku na třetí, nastane konec světa.
Ve skutečnosti hádanka pochází z 19. století a autorem je francouzský matematik Éduard Lucas, uvedená legenda však tvoří tradičně nedílnou součást zadání.

Zadání
Máme tři kolíky, na začátku jsou na jednom z nich nasazeny disky různých poloměrů seřazené od největšího (vespod) po nejmenší (nahoře). Úkolem je přemístit všechny disky na třetí kolík. Je povoleno přesouvat disky pouze po jednom, vždy můžeme vzít pouze horní disk z některého kolíku a přemístit jej na jiný kolík a nikdy nesmíme položit větší disk na menší.
Ztvárnění úlohy
Úloha je řešitelná pro libovolný počet disků, potřebný počet tahů ovšem roste exponenciálně. Pro praktické použití je vhodné používat 3–5 disků. Pro rychlé řešení poslouží mince, pro efektnější ztvárnění můžeme disky nařezat třeba z kulatin různé šířky. Použití 64 zlatých disků silně nedoporučuji.
Úlohu lze využít i jako týmový úkol, konkrétně například takto:
- Disky vyrobíme ve velkém (např. z kartonu).
- Jako kolíky stačí místa označená fáborkem, umístíme je s rozestupy alespoň 1 metr.
- Tým provádí tahy štafetově: člen týmu provede vždy jen jeden přesun, všichni členové týmu se musí pravidelně střídat.
- Tým nesmí v průběhu řešení mluvit, mohou se ale domlouvat gestikulací.
Varianty
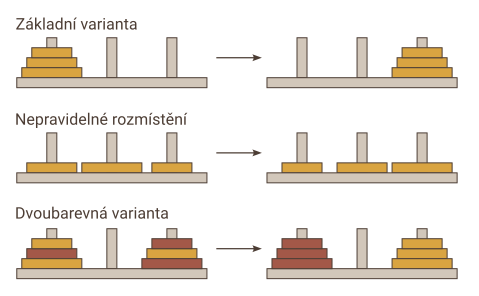
Nepravidelné rozmístění Nyní na začátku kolíky rozhodíme libovolně, ale tak, aby tvořily platnou konfiguraci (vždy menší disk na větším). Cílem je uspořádat kolíky do jiné zadané platné konfigurace, viz příklad na obrázku. Úloha je řešitelná pro libovolné dvě platné konfigurace.
Dvoubarevná varianta Máme dvě sady disků různých barev a úkolem je přeskládat je z přeházeného stavu do uspořádaného (viz obrázek).
Čtyři kolíky Se čtyřmi kolíky je snadnější úlohu vyřešit, ale obtížnější najít optimální řešení – takové, které využívá co nejméně tahů.
Tři příšery
Následující úloha má úplně jiný příběh než základní úloh, ale její vnitřní princip je skutečnosti úplně stejný. V této formulaci je však úloha výrazně těžší, především pokud řešitel o souvislosti neví.
Tři příšery drží tři koule. Jak příšery, tak koule jsou ve třech velikostech: malá, střední, velká. Malá příšera drží velkou kouli, střední příšera drží malou kouli a velká příšera drží středně velkou kouli. Toto uspořádání však uráží smysl příšer pro symetrii, a tak by chtěly situaci změnit do stavu, kdy každá příšera bude držet kouli své velikosti. Příšery mohou měnit velikost koulí, ale musí při tom dodržovat pravidla etikety příšer: 1. V každém tahu se může měnit velikost pouze jedné koule. 2. Pokud dvě příšery drží koule stejné velikosti, jen koule, kterou drží větší příšera, se může změnit. 3. Koule se nikdy nesmí změnit na takovou velikost, jakou má koule, kterou drží větší příšera.
Souvislosti
Rekurze
Úloha Hanojské věže se často používá v informatice při výuce principu rekurze, což znamená „volání sebe sama“. Řešení úlohy pro n disků totiž můžeme zapsat programem na 5 řádků kódu pomocí rekurzivního volání téhož programu pro n – 1 disků. Jde o typickou ukázku elegantního využití rekurze.
Hanojské věže mají také spojitosti s Sierpińského fraktálem a Pascalovým trojúhelníkem. Tyto souvislosti více rozebírám v tomto videu:
Kognitivní věda
Další oblastí, kde hrají Hanojské věže důležitou roli, je kognitivní věda. Herbert Simon, jeden z průkopníků této oblasti, nabízí následující srovnání: „Pokud šachy hrají v kognitivním výzkumu podobnou roli jako Drosophila v genetice, Hanojské věže představují analogii E. coli, poskytující další standardizovaný model, kolem kterého se mohou kumulovat vědomosti.“
Hanojské věže se využívají pro zkoumání toho, jak lidé řeší problémy. Zkoumá se zlepšování dovedností vlivem tréninku, přenos znalostí mezi úlohami či myšlení pacientů s poškozením mozku. Konkrétně se například studuje vliv formulace zadání na způsob a obtížnost řešení problému. K tomu se využívají „izomorfní zadání“, jako je například výše uvedená varianta „Příšery a glóbusy“. Když odhlédneme od „příběhové omáčky“, je prostor platných tahů stejný jako pro klasické Hanojské věže. Pro lidi však není úplně snadné tento vztah odhalit a obtížnost jednotlivých zadání se výrazně liší. Úloha s příšerami trvá lidem průměrně šestnáckrát déle než základní zadání. Proč? Roli hraje způsob, jak lidé přemýšlejí o problémech, využívají omezenou pracovní paměť a další faktory – prostě úloha poskytuje dostatek podkladů pro zajímavý kognitivní výzkum.
